Le Nombre d'Or |
Le Nombre d'Or, une Imposture ? |
M.N. - LE MONDE HISTOIRE & CIVILISATIONS N°19 > Juillet-Août > 2016 |
1,618 : le Mystérieux Nombre d'Or |
TERRA DARWIN N°3 > Mai-Juin > 2019 |
Nombre d'Or |
NATIONAL GEOGRAPHIC N°189 > Juin > 2015 |
Nombre d'Or et Espace-Temps |
COMMENT ÇA MARCHE N°59 > Mai > 2015 |
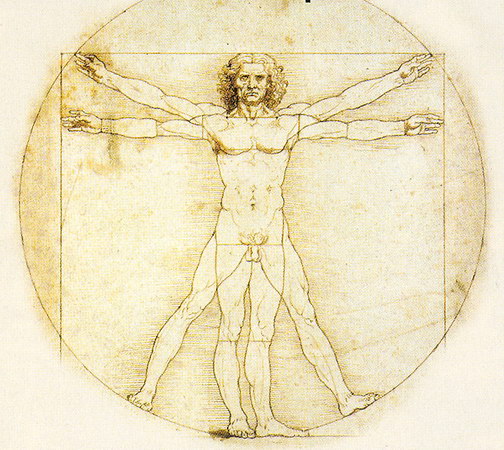
Nombre d'Or : la Divine Proportion |
QUI EST-IL ?
Le nombre d'or est le rapport, ou quotient, entre deux longueurs (L/l) tel que le rapport de la somme des deux longueurs (L+l) sur la plus grande (L) est égal au rapport de la plus grande sur la plus petite (L/l).
Il est souvent désigné par la lettre grecque f, un usage que l'on doit au mathématicien Mark Barr. Il choisit ce symbole notamment en hommage au sculpteur Phidias, qui supervisa les travaux de décoration du Parthénon, et dont la tradition veut qu'il ait utilisé dans ce monument le nombre d'or.
Si l'on nomme x = L/l le quotient que l'on recherche, on peut écrire : x = 1 + 1/x. Le quotient est donc la solution de l'équation x²=x+ 1. Or cette équation du second degré a une unique solution positive : (1 + √5)/2. f est un nombre irrationnel qui vaut approximativement 1,618...
OÙ EST-IL NÉ ?
Euclide mentionne dans ses Eléments le "partage en moyenne et extrême raison" qui définit un rapport entre les segments d'une droite partagée par un point. Ce rapport correspond au nombre d'or, mais il ne sera baptisé ainsi que bien plus tard. Si Euclide le définit, c'est qu'il lui permet de tracer plus facilement des figures géométriques régulières, telle pentagone, ou des polyèdres, comme l'octaèdre (à 8 faces) ou le dodécaèdre (à 12 faces).
OÙ LE TROUVE-T-ON ?
En mathématiques, le nombre d'or a de nombreuses propriétés remarquables. Son carré s'obtient en lui ajoutant 1. Soit φ² = φ + 1. De même, son inverse s'obtient en lui ôtant 1 (1/φ = φ - 1). Plus incongru : en calculant les puissances successives de ce nombre, on voit apparaître la suite de nombres dite de Fibonacci.
De même, comme φ = 1 + 1/φ, si l'on remplace le φ du second membre par son expression (1 + 1/φ), on trouve que φ s'exprime comme une fraction continue, la plus simple qui soit...
Cette simplicité dans l'expression fait du nombre d'or un nombre remarquable entre tous. La définition du nombre d'or permet de jouer ainsi avec de jolies expressions mathématiques.
SES PETITES HISTOIRES
Toute une mythologie est née autour de la signification de ce nombre, de ses supposées propriétés esthétiques, mystiques ou divines. Son histoire est sporadique. Après Euclide, un grand saut dans le temps jusqu'en 1498 nous amène au moine Luca Pacioli, qui publie dans son livre La Divine Proportion des dessins de polyèdres par Léonard de Vinci. L'ouvrage traite des mathématiques appliquées à la proportion artistique et de l'utilisation de celle-ci en architecture. Plusieurs personnages de la Renaissance l'utilisent, tel l'astronome Johannes Kepler, qui concevait l'Univers comme un empilement de polyèdres réguliers et y voyait un arrangement divin. Pas encore d'or dans ce nombre jusqu'au 1854, où le terme "section d'or" apparaît sous la plume du psychologue allemand Adolf Zeising, qui s'intéresse de près aux mathématiques et à la philosophie. Il voit dans cette proportion le sommet de l'esthétique et la distingue partout : dans le frontispice du Parthénon, dans les sculptures grecques ou même dans les cathédrales.
L'idée, reprise et popularisée en 1931 par le diplomate Matila Ghyka, connaît un immense succès. Dans son livre Le Nombre d'or (première apparition de cette appellation), celui-ci invente une histoire mythique du nombre d'or qui aurait été découvert par les Égyptiens, glosant sur un savoir resté secret durant des siècles... Des théories qui ont un écho chez des architectes comme Le Corbusier (1887-1965), qui propose en 1949 le Modulor, un système de proportion basé sur ce nombre. Aujourd'hui, φ est surtout une curiosité mathématique. Il n'en reste pas moins que ses particularités géométriques et son lien avec la suite de Fibonacci lui confèrent un rôle singulier dans la zoologie mathématique.
P.P. - SCIENCES ET AVENIR HS > Octobre-Novembre > 2009 |