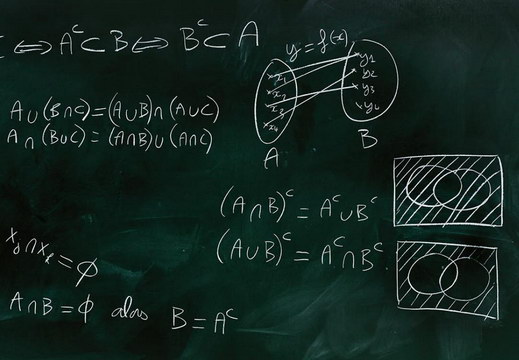Le XXIè Siècle : 7 Idées Neuves |
7/ Penser Types plutôt qu'Ensembles |
Dans les années 1970, les écoliers découvraient les "maths modernes". Intersection, union... toutes les opérations mathématiques devaient désormais s'écrire d'après la théorie des ensembles, fruit d'une conceptualisation amorcée au XIXè siècle. Mais, incomplète et trop abstraite, cette théorie a vite révélé des failles. Or, un autre langage est prêt à prendre le relais. Plutot que de penser les objets mathématiques à partir d'ensembles les contenant tous a priori, ce langage propose de les étiqueter sous forme de "types" permettant ainsi de les classer a posteriori. Un fantastique gage de souplesse, à l'instar des langages informatiques, qui donne des résultats théoriques. C'est sûr, les maths par types ont l'avenir devant elles ! Les écoliers du XXIè siècle ne s'en plaindront pas...
Combien d'élèves ont souffert de l'introduction des "maths modernes" dans les années 1970 ? Cet enseignement voulait faire partager aux élèves une ébauche de ce qui constitue le fondement des mathématiques contemporaines : la théorie des ensembles. Si cette réforme fut finalement abandonnée durant les années 1980 - on lui reprocha son excès d'abstraction, son élitisme, le manque de formation des enseignants -, elle eut l'avantage de mettre sur le devant de la scène cette notion pourtant simple et intuitive, au rôle si prépondérant. Tout le monde a une idée de ce qu'est un ensemble : une collection d'objet pour certains, une patate avec des points dedans représentant ses éléments pour d'autres. Et, les élèves des années 1970 ont appris comment ces patates peuvent allègrement être mélangées, au gré d'unions et d'intersections, pour reconstruire tous les objets usuels des mathématiques (fonctions, entiers naturels, transformations géométriques...), au fil d'une implacable logique, décrite sur le tableau noir en quelques lignes formelles, qui en ont laissé plus d'un interdit.
Eh bien, ceux qui sont encore hantés par cette théorie des ensembles peuvent se réjouir : de plus en plus de mathématiciens sont convaincus que l'heure est venue de changer les fondations. Un petit groupe d'une trentaine de mathématiciens et d'informaticiens de haut niveau vient ainsi de passer une année à l'Institut des études avancées de Princeton, dans le but de réécrire l'intégralité des théories mathématiques non pas à l'aide de la notion d'ensemble, comme cela a été fait durant tout le XXè siècle, mais à l'aide d'une autre notion, appelée à marquer tout autant le XXIè siècle : celle de "type". "Nous voulons comprendre si cela se passerait mieux si l'on réécrivait la présentation systématique des mathématiques en se basant sur la théorie des types plutôt que sur la théorie des ensembles", résume de façon lapidaire Assia Mahoubi, jeune chercheuse au centre Inria de Saclay, qui participe au séminaire de Princeton. À la clé ? Des perspectives radicalement nouvelles sur les mathématiques, sur le sens à dormer à cette pratique multimillénaire, sur la façon de les pratiquer aujourd'hui, sur la manière de les enseigner... Ce pourquoi, loin de n'être un enjeu que pour les rares spécialistes du sujet, ces joutes vertigineusement abstraites concernent tout le monde.
Type et ensemble, quelle différence ? De manière sous-jacente, il s'agit dans les 2 cas de classer les objets ; mais autant l'une invite a dessiner des patates, autant l'autre pousse à coller des étiquettes. "Qu'est-ce que l'ensemble des chats verts, demande le mathématicien Pierre Cartier pour illustrer plus subtilement cette différence. Premier point de vue, celui des contes de fées : le roi, qui veut faire un discours à tous les chats verts de son royaume, dépêche des hérauts dans le pays, leur demandant de trouver tous les chats verts et d'exclure les autres, puis de les rassembler le jour dit, à l'heure dite, dans la salle du château. L'ensemble des chats verts est alors constitué des éléments qui sont dans la pièce quand le roi fait son discours. L'autre manière de voir l'ensemble des chats verts, c'est celle de l'entomologiste. Il y a quelque part au Museum un casier où il est indiqué 'chat vert'. Chaque fois qu'un correspondant, n'importe où dans le monde, trouve un chat vert, il l'envoie à l'entomologiste, qui le met dans le casier".
Cette différence de conception oppose un ensemble en extension (conte de fées) et un autre défini en comprehension (entomologie). Alors que, dans la première manière de voir, caractéristique de la théorie des ensembles, l'ensemble des chats verts n'a d'existence qu'après la convocation du roi, une fois tous les spécimens réunis, la seconde conception, typique de la théorie des types, laisse la collection se constituer progressivement. Un type, ce n'est pas la réunion de tous les objets possédant une certaine caractéristique (par exemple l'ensemble de tous les entiers naturels), mais une sorte de boite dans laquelle on peut faire entrer les objets qui ont le bon format (par exemple le type des entiers naturels). Or, vouloir rebâtir toutes les mathématiques à partir de ce concept, c'est faire la révolution.
Pour comprendre, il faut revenir au debut de l'histoire, lorsque la théorie des ensembles prétend être aux fondements des mathématiques. En commençant par les prémices, posées par Georg Cantor. À la fin du XIXè siècle, le mathématicien allemand développe des méthodes pour compter les éléments, fussent-ils en nombre infini. Son principe : deux ensembles ont la même taille si chaque élément de l'un peut être mis en relation exclusive avec chaque élément de l'autre. Ne pouvant mettre en relation chaque nombre entier avec chaque nombre réel, il en déduisit qu'il y a infiniment plus de réels que d'entiers : l'ensemble des nombres réels n'est pas dénombrable. La notion d'ensemble fait dès lors une entrée tonitruante en mathématique. Ce qui crée tout de suite des tensions.
Le logicien Bertrand Russell met ainsi en évidence dès 1903 un paradoxe de la théorie : l'existence de l'ensemble de tous les ensembles est contradictoire. Et le mathématicien anglais résout lui-même ce paradoxe en introduisant... la théorie des types. Il propose que chaque objet soit défini par une sorte d'étiquette qui détermine la façon dont il peut être combiné avec d'autres. Mais ce premier combat entre types et ensembles va tourner court. D'abord parce que la theorie des types de Russell, qui culmine dans son ouvrage écrit entre 1910 et 1913 avec Alfred Whitehead, Principia Mathematica, est trop lourde à mettre en ouvre - elle ne permet de déduire 1+1=2 qu'après 362 pages de déductions formelles laborieuses... Ensuite parce que, en face, les critiques font réagir : en 1908, Ernest Zermelo publie son premier système d'axiomes - des vérités indémontrables qui doivent être admises - pour bâtir des résultats pressentis par Cantor. C'est le véritable acte de naissance de la théorie des ensembles qui est formellement très éloignée de la théorie "naïve" enseignée à l'école. Ce système ensuite amélioré, connu depuis sous le nom de système ZFC, va permettre à la théorie des ensembles de devenir le système de référence dans lequel, in fine, tout doit pouvoir s'exprimer, l'algèbre aussi bien que la géométrie ou l'analyse (tout en résolvant le paradoxe de Russell). Durant les premières décennies du XXè siècle, c'est sous l'impulsion de David Hilbert que va peu à peu s'imposer cette théorie. "Hors du paradis de Cantor, nul ne nous chassera". Le géant allemand rêve de mathématiques dont les fondements seraient exempts de paradoxes et de contradictions, où tout résultat pourrait se déduire de manière purement logique, sans faille possible dans le raisonnement. La théorie des ensembles, avec son système ZFC, lui semble parfaite pour ce programme.
Certains, comme Henri Poincaré, l'autre grande figure tutélaire des mathématiques de l'époque, émettent cependant encore des doutes sur le risque de cercles vicieux dans le raisonnement ou sur l'utilisation qu'il y est fait de l'infini : "Aucune proposition concernant les collections infinies ne peut être évidente par définition". Le mathématicien s'amuse par avance des difficultés qu'il y aura à tout rebâtir. La suite de l'histoire lui donnera raison... Cette vision fondamentale de la théorie des ensembles va d'abord être confrontée aux sévères critiques de Luitzen Brouwer. Dans les années 1920, la mathématicien néerlandais exige de ses pairs, s'ils veulent éviter tout raisonnement vicié, de ne parler que de ce qu'ils peuvent effectivement construire. Brouwer s'interdit en particulier le raisonnement par l'absurde, qui permet de manipuler des objets qui n'existent pas. Dans le courant des mathématiques qu'il fonde ainsi, baptisées "intuitionistes", ou "constructivistes", la théorie des ensembles est exclue des fondations. Comment le roi peut-il être sûr que les chats verts sont bien au complet dans la salle du chateau ? Luitzen Brouwer préfère la prudence de l'entomologiste qui remplit au fur et à mesure ses tiroirs étiquetés. Pour la seconde fois, les types défient les ensembles. Combattu par Hilbert, ce courant, reste cependant très minoritaire.
PAS EXEMPT DE FAILLES
La théorie des ensembles va même résister aux fracassants résultats obtenus par Kurt Godel au début des années 1930. En démontrant qu'une formalisation logique complète et consistante des mathématiques est impossible, le logicien autrichien met à bas le programme d'Hilbert. De quoi saper l'idéal de la recherche de fondements logiques universels. Mais le résultat est en accord avec l'expérience de beaucoup de mathématiciens sur l'inutilité pratique de telles formalisations (les 362 pages de Russell et Whitehead pour déduire 1+1=2 en étant une parfaite illustration). Et si la question des fondements devient peu à peu secondaire. la théorie des ensembles reste, par consensus, le paradigme dominant, les mathématiciens se contentant de cette formalisation imparfaite mais efficace. "Malgré les critiques de Bromver, de Poincaré, et d'autres très grands, malgré le théorème d'incomplétude de Godel qui a miné le progmmme de Hilbert dans sa forme originale, c'est le formalisme version Hilbert qui l'a emporté", résume Henri Lombardi, mathématicien constructiviste de longue date. La preuve : à partir de la fin des années 1930, ce sont des bases ensemblistes que le groupe de mathématiciens Bourbaki a utilisées dans son ouvrage colossal et collectif Eléments de mathématique, dont l'ambition est de présenter toutes les mathématiques contemporaines, et dont le dernier volume fut publié... en 1998.
Pourquoi ce paradigme a-t-il finalement été adopté de manière quasi universelle, malgré ses défauts ? "Sans doute parce que c'était le système le plus simple", estime Pierre-Louis Curien, logicien au Laboratoire PPS de l'université Denis-Diderot (Paris VII). Même s'il n'est pas exempt de failles, les mathématiciens disposent là d'un système construit avec la plus simple des logiques, qui leur offre un bon cadre pour traduire leurs intuitions, en leur laissant toutes leurs armes, comme le raisonnement par l'absurde. Bien sûr, aujourd'hui, bien peu de mathématiciens connaissent les axiomes de base de cette théorie : ils l'utilisent de manière intuitive, un peu comme Monsieur Jourdain faisait de la prose sans le savoir. Mais la facilité avec laquelle sa syntaxe traduit les raisonnements a finalement jeté un voile pudique sur les problèmes de sémantique - quel est le sens de ce langage ? Quel statut confère-t-il aux travaux mathématiques ? Que dit-il de l'activité des mathématiciens ? Ce pragmatisme n'a cessé de nourrir des réticences d'ordre philosophique. "Une théorie sans sémantique sérieuse, la théorie ZFC, a semblé préférable à la communauté, déplore Henri Lombardi. On renvoyait les problèmes de fond à plus tard - en gros : seulement si des contradictions apparaissaient. Pourtant qu'est-ce qu'une théorie formelle sans sémantique sérieuse, sinon quelque chose de profondément creux. Dans l'introduction de son monumental traité, Bourbaki présente 'la' (et non pas les) mathématique comme un pur jeu formel. C'est vraiment tomber bien bas !"
À partir des années 1960, le principal problème auquel est confrontée la théorie des ensembles devient cependant d'ordre purement mathématique : cette théorie se marie mal avec le nouvel objet phare des mathématiques, la notion de "catégorie". Il faut dire que cette notion atteint des sommets de l'abstraction. Les catégories sont des collections de structures. Par exemple, on peut considérer la "catégorie des groupes" - la structure mathématique la plus élémentaire en prenant la collection de tous les groupes possibles. L'idée est ensuite d'étudier les propriétés de cette sorte de "structure de structure". Cette notion imaginée dans les années 1940 sera rendue encore plus abstraite durant les années 1950 et 1960 sous l'impulsion d'Alexander Grothendieck, qui n'hésite pas à considérer des "catégories de catégories", des "catégories de catégories de catégories", etc. Le problème est que ces notions deviennent si abstraites qu'il devient délicat de les exprimer en théorie des ensembles. Ce qui suggère que cette dernière ne serait peut-être pas le bon cadre fondamental. À l'époque, les mathématiciens se demandent même s'il ne convient pas de donner aux catégories la place centrale qu'occupent les ensembles. Faut-il refondre les 20 volumes de Bourbaki déjà parus et qui étaient écrits dans un carcan très rigide ? "Remettre les catégories au premier rang aurait obligé à tout refaire et après des discussions qui ont duré presque 8 ans, ce sont les conservateurs qui ont gagné, de sorte que Bourbaki a gardé ses bases ensemblistes", raconte Pierre Cartier. C'est un nouveau rendez-vous manqué pour la théorie des types, susceptibles d'exprimer plus efficacement les catégories de Grothendieck. Et c'est à cette époque, malgré tous ses défauts, que la théorie des ensembles envahit les salles de classe, du primaire au lycée, avec le succès pédagogique que l'on sait... De son côté, la théorie des types, délaissée pendant des décennies, commence à revenir sur le devant de la scène. Les premiers intéressés par résurgence sont en fait les informaticiens. La notion de type permet en effet de classer efficacement les objets définis dans les programmes informatiques. "Expérimentalement, les types étaient un bon moyen de trouver les erreurs de progmmmation avant de lancer l'exécution d'un programme", explique Thierry Coquand, informaticien à l'université de Goteborg (Suède). Un hesoin qui n'a fait que s'amplifier avec la taille croissante des programmes.
L'APPORT DÉCISIF DE COQ
Les travaux en logique pure constituent l'autre moteur de la renaissance des types. Une renaissance portée par la découverte à la fin des années 1960 d'une profonde correspondance entre les programmes informatiques et les démonstrations mathématiques, la "correspondance de Curry-Howard". Cette correspondance stipule qu'en utilisant le langage des types, les preuves peuvent se lire comme des programmes. Le langage inventé par Russell est alors mûr pour sortir du bois. Plusieurs théories des types sont imaginées, comme le très élégant système F du logicien Jean-Yves Girard. Mais c'est finalement le Suédois Per Martin-Lof qui élabore, dans les années 1970, la théorie des types que nous connaissons aujourd'hui. Un formalisme conçu pour mettre en pratique la correspondance preuve-programme.
Un pas décisif sera réalisé dans les années 1980 par 2 informaticiens français : Gérard Huet et son étudiant en thèse Thierry Coquand. "Avec notre 'calcul des constructions', nous cherchions comment utiliser la théorie des types pour représenter des preuves mathématiques sur ordinateur, mais aussi pour développer des programmes, raconte Thierry Coquand. Nous voulions un formalisme qui fonctionne pour représenter à la fois des preuves mathématiques et des programmes, avec l'idée, sans doute un peu naive alors, d'unifier math et informatique". L'assistant de preuve ainsi conçu, baptisé Coq par Gérard Huet, va se révéler très efficace. Il permettra en 2005 à l'équipe de Georges Gonthier et Benjamin Werner de verifier sur ordinateur un théorème fameux, bien que secondaire, le "théorème des 4 couleurs". Puis, en 2012, le théorème de Feit-Thompson, un résultat de l'algèbre du XXè siècle cette fois-ci majeur. "Ce qu'a fait Georges Gauthier est pour moi un bon exemple d'unification entre mathématique et informatique, car il a dû réexprimer des concepts mathématiques de manière informatique. Et cela a été utile pour avoir de meilleures preuves", estime Thierry Coquand. Reste à voir si tout le reste des mathématiques se laisse aussi traduire à l'aide de la théorie des types.
Cette approche ranime inévitablement la vieille querelle des fondements des mathématiques. Elle s'inscrit dans le droit d'un Russell voulant éviter les risques de cercle vicieux que présente la théorie des ensembles, ou d'un Brouwer intimant l'ordre de ne raisonner qu'en utilisant des procédures de calculs effectivement réalisables. Et, grâce aux ordinateurs, elle n'est plus aussi lourde et paralysante que par le passé. La grande révolution des fondements des mathématiques est-elle, cette fois-ci, en branle ? Après tant de tentatives infructueuses, l'heure est-elle venue, pour les mathématiciens, de penser types plutôt qu'ensembles ? C'est pour répondre à cette question que s'est organisé à partir de septembre 2012 le séminaire spécial à l'Institut des études avancées de Princeton. Mais c'est en fait autour d'une découverte venue d'un domaine mathématique totalement différent que toutes les discussions ont tourné. Une découverte qui laisse penser que la théorie des types est justement prête à passer à des niveaux d'abstraction supérieurs, de représenter des notions plus élaborées, comme les catégories, et étendre ainsi son champ sur tout le paysage mathématique.
Le domaine en question est l'homotopie, c'est-à-dire l'étude des déformations continues d'un objet à un autre, comme l'étude des formes que peut prendre un lacet dont les extrémités sont fixées en deux points d'un espace. Rien à voir a priori avec la logique et l'informatique... Pourtant, Vladimir Voievodski, l'un des meilleurs spécialistes au monde de l'homotopie, a remarqué une correspondance inattendue. Une correspondance qui permet de définir de façon très élégante l'égalité entre deux types. A et B étant 2 types, quand peut-on dire que A=B ? Déroutante de simplicité, la question était justernent l'un des points d'achoppement dans les assistants de preuve. Car le statut de l'égalité est très contraignant. Et lorsque les notions deviennent trop conceptuelles, les informaticiens sont à la peine pour bien la définir. Quels axiomes faut-il prendre sur l'égalité entre deux types d'être en mesure de représenter les notions mathématiques les plus sophistiquées ? Il y a une dizaine d'années, avec plusieurs chercheurs dont le philosophe Steve Awodey de l'université Carnegie-Mellon à Pittsburgh, Vladimir Voievodski a observé que la notion d'égalité en mathématiques, telle qu'elle existe dans la théorie des types de Martin-Lof sur laquelle est fondée Coq, se comporte exactement comme la notion de chemin entre 2 points en théorie de l'homotopie. Autrement dit, 2 types sont égaux à la manière que le sont 2 formes que peut prendre un lacet fixé à ses extrémités. Ce qui lui a permis de proposer un axiome, "l'axiome d'univalence", permettant, de définir de façon très générale quand est-ce que l'on peut dire que 2 types sont égaux. Un axiome beaucoup moins rigide que les précédents qui promet une utilisation plus intuitive de la théorie des types, plus proche du travail mathématique usuel. Ce qui rend le système axiomatique de la théorie des types en mesure d'affronter le fameux système ZFC.
Ce sont ces liens entre homotopie et type qui ont animé le séminaire de Princeton organisé par Voievodski, Coquand, Awodey, baptisé "Fondation univalente des mathématiques". "La discussion a beaucoup porté sur cette notion d'égalité. Philosophiquement, nous aimerions justifier de manière intuitive l'ajout de l'axiome d'univalence à la théorie des types. Et je dois dire qu'après un an de discussion, ce n'est pas encore clair", avoue Thierry Coquand. Reste que les résultats sont déjà prometteurs. Certains théorèmes ont pu être redémontrés de manière nouvelle, purement logique, à partir de cette nouvelle expression de l'égalité en théorie des types. Avec cette connexion qui relie 2 domaines complètement différents, on sent que l'on met le doigt sur quelque chose de profond, reprend Thierry Coquand. Cette connexion permet une formalisation logique directe de concepts importants qui peuvent être appliqués à de vastes champs des mathématiques. La fameuse notion d'ensemble peut être à partir des fondations univalentes partant de concepts plus primitifs récemment découverts par Vladimir Voievodski".
Et même les sommets de l'abstraction mathématique semblent maintenant à portée. "L'un des résultats très prometteur de ces mois de travail a consisté à formuler certaines catégories à l'aide de la théorie des types en utilisant la notion d'égalité mise en avant par Voievodski", explique Pierre-Louis Curien. Algèbre, catégories, ensembles, les places fortes des mathématiques semblent tomber une à une. Et Vladimir Voievodski en est persuadé : "La notion de type va permettre de représenter de manière plus efficace les mathématiques contemporaines. Dans cette nouvelle rencontre au sommet entre la théorie des types et celle des ensembles, le combat n'est pas encore véritablement engagé - les tenants de la théorie des types fourbissent toujours leur arsenal axiomatique et la formalisation reste un travail de titan. Mais jamais la première n'a semblé aussi bien armée, et jamais la seconde ne l'a semblé aussi peu. Et il est d'ores et déjà possible d'imaginer les conséquences d'un tel changement de régime. D'imaginer à quoi pourraient ressembler les mathématiques reconstruites sous l'égide de Poincaré, Russell et Brouwer, comparées celles imposées par Hilbert, Zermelo et Bourbaki.
UNE AUTRE RÉFORME DES MATHS ?
Ce changement dans les fondements consacrerait d'abord le rapprochement des mathématiques et de l'informatique, 2 cultures qui, jusqu'à une période récente, ont suivi des voies plutôt séparées. Ce rapprochement, en soi, n'est guère étonnant : les programmes de nos ordinateurs ne sont-ils pas les descendants des systèmes logiques imaginés par les mathématiciens dans leur recherche des étapes élémentaires du raisonnement ? Mais il est devenu depuis peu d'ordre culturel : "Les jeunes matheux qui arrivent savent programmer, perçoit Pierre-Louis Curien. Ces jeunes ne se posent plus la question de savoir s'ils sont mathématiciens ou informaticiens : ils manipulent les deux avec aisance". Un cocktail potentiellement explosif. Cette fusion avec l'informatique transformerait à coup sûr la façon dont les mathématiques se pratiquent. On verrait le foisonnement de ces nouveaux outils que sont les assistants de preuve, capables de suivre le raisonnement du chercheur, de le vérifier, voire de le guider. "Les assistants de preuve nous laissent espérer de faire des mathématiques de manière plus décentralisée, un peu comme le font ceux qui fabriquent du logiciel libre", explique Paul-André Melliés, logicien à l'université Denis-Diderot. "En particulier, on n'aura plus besoin de l'avis de spécialistes d'un domaine pour savoir qu'un résultat est vrai. Et, comme dans un logiciel libre, on peut imaginer que des démonstrations soient construites par petits bouts à partir d'une architecture que quelques experts [ou pas] auraient pu mettre en place". Ces mathématiques formalisées à l'aide de la théorie des types ne seraient alors probablement plus exactement les mêmes. Nettoyées, plus effectives, elles jetteraient un regard novateur sur les résultats classiques. Si Voievodski s'est engagé dans cette aventure, c'est d'ailleurs avant tout dans l'espoir d'obtenir des résultats nouveaux en théorie de l'homotopie, grâce aux raisonnements logiques que la théorie des types et l'univalence permettent d'introduire.
D'un point de vue plus philosophique, les mathématiques pourraient se targuer de remporter l'adhésion grâce à un raisonnement fondé sur la seule logique - et non sur l'existence d'objets, comme l'ensemble des chats verts. Ce qui signerait la victoire des mathématiques constructivistes si longtemps marginalisées. "Les mathématiques non constructivistes auraient été alors juste une manière de survoler les obstacles, lâche Henri Lombardi, rêveur. La communauté, après 1 ou 2 siècles d'errance, retomberait sur ses pattes, comme le souhaitait Poincaré". Et il restera finalement, à se demander en quoi la révolution des types pourrait influencer l'enseignement. Faudrait-il une nouvelle réforme des maths modernes ? Faudrait-il intégrer les types dans les manuels scolaires ? Au final, de toutes les questions soulevées par ces batailles épiques, celle-ci n'est sûrement pas la moins complexe...
7 Idées Neuves pour le XXIème Siècle |
|
7/ MATHS : Penser Types plutôt qu'Ensembles |
P.P. - SCIENCE & VIE > Octobre > 2013 |